Перегрузка и охлаждение ионов Yb⁺ в комбинированной квадрупольно-мультипольной ловушке для реализации микроволнового стандарта частоты

А. Е. Корольков^1,3, И. Журавлев^1,2, К. Павленко⁴, И. А. Семериков^1,3, И. В. Заливако^1,3, А. С Борисенко^1,3, М. Д. Аксенов^1,3, П. Л. Сидоров¹, Н. В. Семенин¹, В. Н. Смирнов^1,2,3, К. Ю. Хабарова¹, Н. Н. Колачевский^1,3

¹ФИАН, г. Москва, Россия

⁴АО «Время-Ч», г. Нижний Новгород, Россия

Использование мультипольных ловушек в ионных стандартах частоты позволяет существенно снизить влияние эффекта Доплера второго порядка на характеристики стандарта. В данной работе мы численными методами проводим сравнение плотности распределения ионов в квадрупольной и мультипольной ловушке, а также сравнение сдвига частоты из-за эффекта Доплера второго порядка от микродвижений ионов в данных ловушках. Полученные результаты показывают преимущества мультипольных ловушек. Также мы демонстрируем экспериментальную реализацию комбинированной квадрупольно-мультипольной ловушки с возможностью перегрузки ионов между ними.

Линейные ловушки Паули часто используются для захвата заряженных частиц и проведения экспериментов в области спектроскопии и квантовой логики. Удержание заряженных частиц с зарядом ⁺e и массой m в таких ловушках, имеющих 2k электродов, описывается с помощью следующего псевдопотенциала в радиальном направлении вблизи оси ловушки [1]:

где V₀ — амплитуда переменного напряжения на электродах ловушки,

Ω — его угловая частота,

r₀ — внутренний радиус ловушки.

В то же время концентрация ионов в таком потенциале описывается распределением Больцмана:

\( \psi (r)=\frac{k^2}{4}\frac{e^2}{mΩ^2}\frac{V^2_0}{r^2_0}{\ \hat{r}}^{2k-2},\ \hat{r}=\frac{r}{r_0}, \)

где k_B — постоянная Больцмана.

\( n(r)=n(0)exp{\frac{-ψ(r)-eφ(r)}{k_BT}}, \)

С учетом уравнения Пуассона, связывающего концентрацию ионов с потенциалом φ(r), можно получить, что концентрация ионов в ловушке удовлетворяет следующему уравнению [2]:

\( n{\rm ''(}r{\rm )+}\frac{n{\rm '(}r{\rm )}}{r}{\rm -}\frac{{n{\rm '(}r{\rm )}}^{{\rm 2}}}{n{\rm (}r{\rm )}}{\rm -}\frac{{n{\rm (}r{\rm )}}^{{\rm 2}}}{n_0λ_D}{\rm =-}k^{{\rm 2}}{{\rm (}k{\rm -}{\rm 1)}}^{{\rm 2}}\frac{n{\rm (}r{\rm )}}{{\rm 4}λ^{{\rm 2}}_D}{\hat{r}}^{{\rm 2}k{\rm -}{\rm 4}}. \)

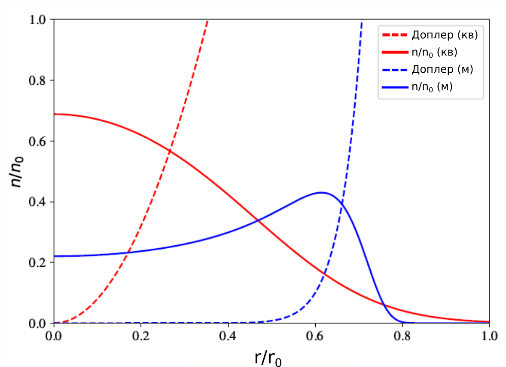
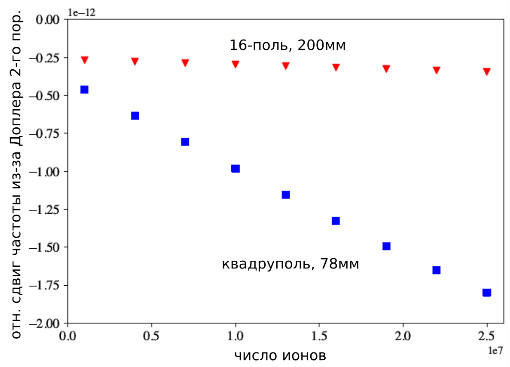
Мы численно решили это уравнение для квадрупольной и мультипольной ловушки с 16 электродами и оценили вклад ионов на разных расстояниях от оси ловушки в сдвиг частоты из-за эффекта Доплера второго порядка (рис. 1 а), а также зависимость этого сдвига от числа ионов в облаке (рис. 1 б).

а)	б)
Рис. 1. Сдвиг частоты из-за эффекта Доплера второго порядка: а) вклад ионов на разных расстояниях от оси ловушки в сдвиг частоты, б) зависимость сдвига частоты от числа ионов в облаке

В нашей экспериментальной реализации мы используем комбинированную ловушку, состоящую из квадрупольной секции с хорошим оптическим доступом и мультипольной секции с 16 электродами, использующую описанные выше преимущества. Такую ловушку предполагается использовать для создания микроволнового стандарта частоты на ионах, где подготовка и считывание состояния ионов происходит в квадрупольной секции, а взаимодействие ионов с микроволновым полем — в мультипольной секции, что позволит снизить влияние эффекта Доплера второго порядка как основного вклада в систематическую погрешность определения частоты перехода.

Литература

1) Gerlich D. Inhomogeneous RF fields: a versatile tool for the study of processes with slow ions // Advances in chemical physics. 1992. Vol. 82. P. 1–176.

2) Prestage J. D., Tjoelker R. L., Maleki L. Higher pole linear traps for atomic clock applications // Proceedings of the 1999 Joint Meeting of the European Frequency and Time Forum and the IEEE International Frequency Control Symposium. 1999. Vol. 1. P. 121–124.